2D Physics Simulaion
Project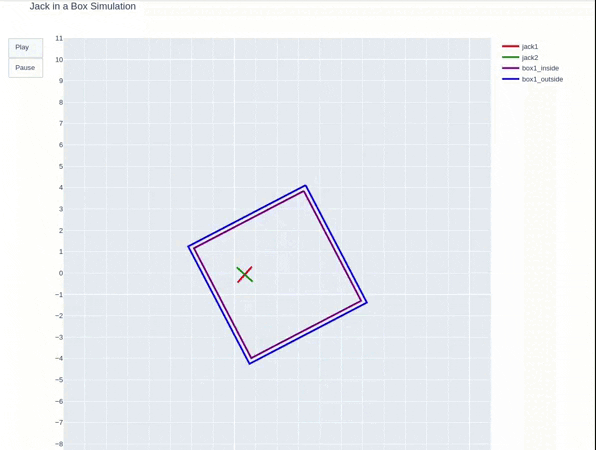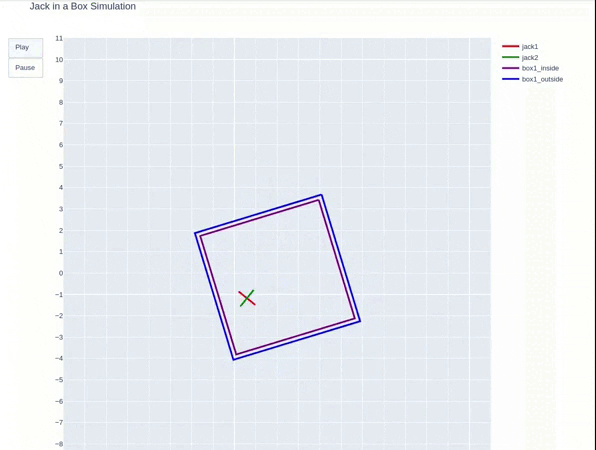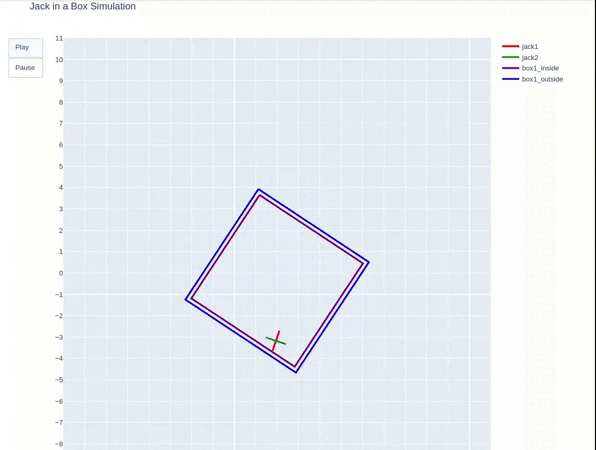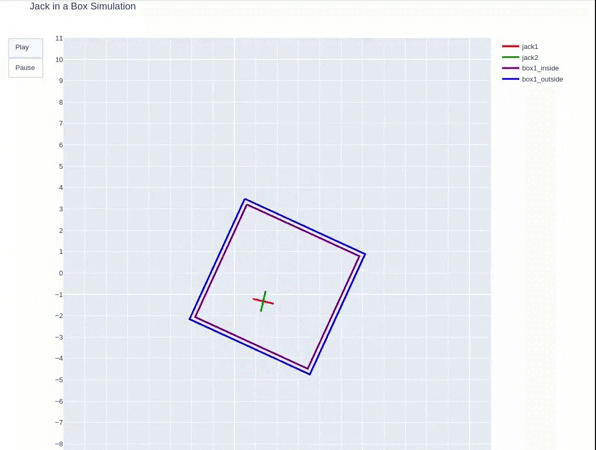
A dice bouncing inside a box
Project
This project simulates the 2D dynamics of dice in the box. In this simulation, a dice is falling freely into the box while an external force react is on the box. The dice will experience collision when it contacts the box edges.
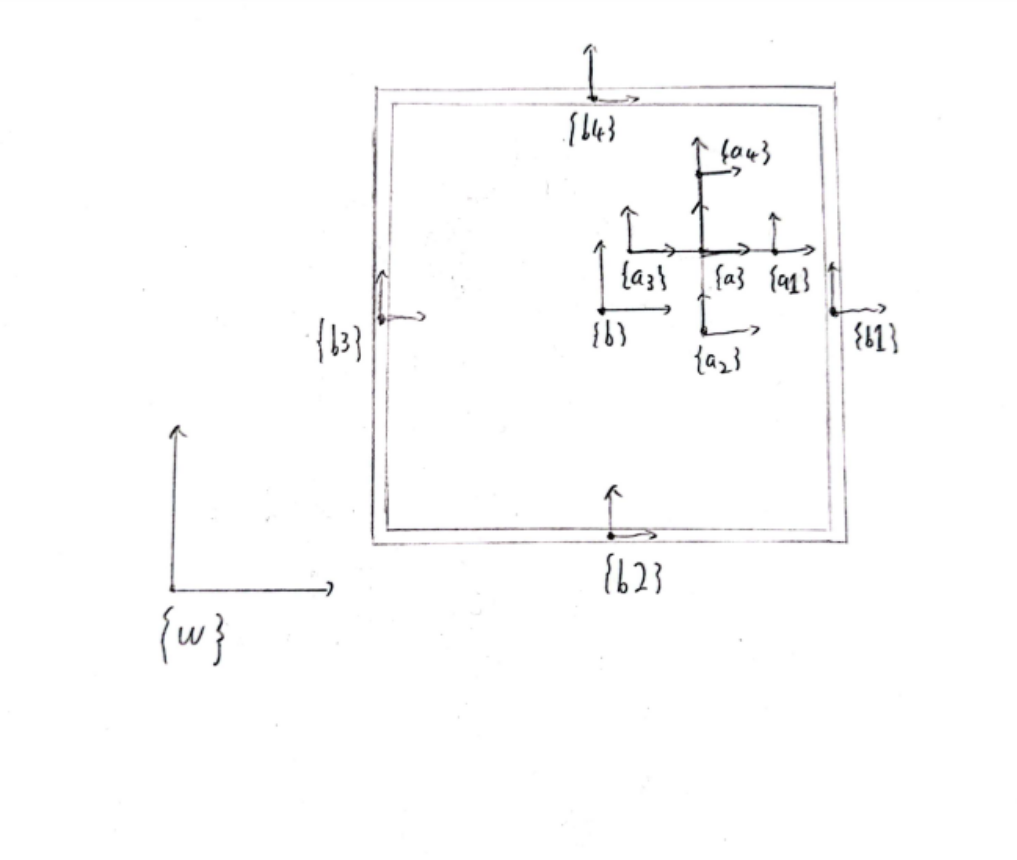
System schematic
The Lagrangian dynamics is used for this project. To construct the Euler-Lagrange equations, we need to know Lagrange equations and External forces in the system. To simplify Euler-Lagrange equations, all frames will be expressed in the world frame. The Lagrange equation is composed of two components: kinetic energy and potential energy. The kinetic energy can be expressed as 0.5*Vb.transpose()*M*Vb (In python) for each mass in the system. The Vb is the frame velocity and M is the Mass matrix. The potential energy can be expressed as m*g*y for each frame, in which m is the mass, g is the gravitational acceleration, and y is the position in the y direction in the world frame. We can get the Lagrange equation for our system after we defined kinetic energy and potential energy. We know the q includes xa, ya, theta_a, xb, yb, theta_b, and this can be used to calculate the dLdqdot and dLdq. Now the left side of the Euler-Lagrange equation can be constructed. The right side is just the force that we defined. By combining the left and right sides of the equation, the Euler-Lagrange equation is constructed.
The constraints can be determined by checking the position of frame a1, frame a2, frame a3, and frame a4 in frame b1, frame b2, frame b3, and frame b4. Because the walls on the box have width, the limitations in b1, b2, b3, and b4 are different. The position can be found by frame transformation. For example, we can use the g_b1a1[1][3] to determine the y position of a1 in frame b1. If the position of a1, a2, a3, and a4 reached the limitation, the impact function will be initialized to update the impact.
To update impacts, we need following equations to construct our impact equation for each impact condition:
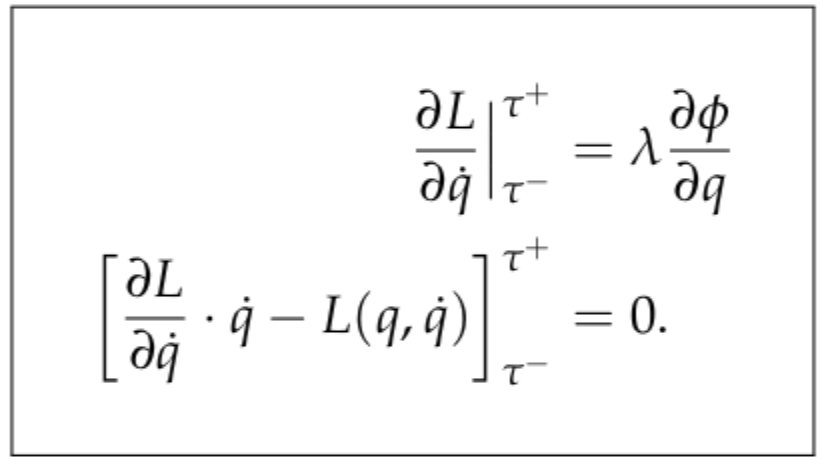
Impact Equations
In this equation, dLdqdot, L, and qdot are constructed previously. Lambda is an unknown variable. Phi is our constraint. Combining all the functions together by substituting variables with the correct sign, we can get the impact update equations for each impact condition. When impact happened, we substitute the current pose and velocity into the function and solve them numerically for the updated velocity.
More information and source code can be found on the project's GitHub repository.